

This is the translation of a talk given in French during the French Perl Workshop in 2009. There are a few differences with the original talk. Since I have no time limit for this HTML file, there are a few points which were skipped during the talk. And also, a few points I did not dig enough before the conference and which I fixed later.

Source: personal picture
Karl Menninger, Number Words and Number Symbols, A Cultural History of Numbers, Dover Publications, translation of Zahlwort und Ziffer: Eine Kulturgeschicht der Zahlen, 1957.
Geneviève Guitel, Histoire comparée des numérations écrites, Flammarion publisher, 1975.
Georges Ifrah, Histoire universelle des chiffres, Seghers, 1981, an English translation exists.Plus Wikipedia, but only for some pictures, not for the articles.
Let us note that Karl Menninger is a linguist, which is why he is interested in spoken as well as written numbers. Geneviève Guitel and Georges Ifrah are mathematicians and are therefore mostly interested in written numbers. In the following text, I quote these three books by the initials of the author and the page number. If you have a different edition (the English translation of Georges Ifrah's book, for example), well, too bad for you, you will have to guess!
use Roman;
for my $ar (qw/1 5 8 40 84/) {
my $rm = Roman($ar);
print "$ar -> $rm\n";
}
for my $rm (qw/I IV VII XIV LII LXXXIV/) {
my $ar = arabic($rm);
print "$rm -> $ar\n";
}
use Math::Roman;
for (qw/1 5 8 40 84 I IV VII XIV LII LXXXIV/) {
my $roman = Math::Roman->new($_);
my $arab = $roman->as_number;
print "$arab -> $roman\n";
}
This module allows you to redefine the characters used for roman numbers. Here is an example from the module's POD, where 25 is written "AAB", with "A" for 10 and "B" for 5:
Math::Roman::tokens ( qw(A 10 B 5) );
$r = Math::Roman::roman('AAB');
print "'$r' is ",$r->as_number(),"\n";
In the following, I will differentiate between the "basic" variant and the "advanced" variant. The basic variant does not use the tokens function, while the advanced variant uses it.
use Text::Roman;
for my $ar (qw/1 5 8 40 84/) {
my $rm = roman($av);
print "$ar -> $rm\n";
}
for my $rm (qw/I IV VII XIV LII LXXXIV xiv lii lxxxiv /) {
my $ar = roman2int($rm);
print "$rm -> $ar\n";
}
I nearly missed this module, because I equated "Roman" to "Latin" and the association between "Text" and "Roman/Latin" makes me think of the ISO-8859-1 encoding.
use Convert::Number::Roman;
use utf8;
for my $av (1, 5, 8, 40, 84,
"Ⅰ", "Ⅹ", "ⅬⅢ", "ⅩⅭ",
) {
my $cnr = Convert::Number::Roman->new($av);
my $ap = $cnr->convert;
print "$av -> $ap\n";
}
At last a module which is compatible with the theme of YAPC::Europe 2011, "Modern Perl". Not only this is a recent module (first released in July 2011), but it is also a modern module, which requires Perl 5.14.0.
use utf8;
use feature ':5.14';
use Roman::Unicode qw/to_roman is_roman to_perl/;
for (qw/1 3 26 84 1234 4321 12345 64321 222333/) {
my $r = to_roman($_);
say $_, ' ', $r;
}
for (qw/Ⅰ ⅠⅠⅠ ⅩⅩⅤⅠ ⅬⅩⅩⅩⅠⅤ/) {
if (is_roman($_)) {
my $n = to_perl($_);
say $_, ' ', $n;
}
else {
say "$_ invalid roman number";
}
}
use Acme::Roman; my $a = LXX; my $b = XIV; print $a + $b, "\n";
This module requires Roman.pm and adds some AUTOLOAD magic, therefore the limits of Roman.pm described below apply also to Acme::Roman.
Even without an Acme prefix, Lingua::Romana::Perligata is another module "for fun", written by Damian Conway. The current version is 0.50. Example:
use Lingua::Romana::Perligata; cumula meis listis III tum IV tum XC tum LX. per quisque nombrum in listis fac sic nombrum tum novumversum egresso scribe. nombrum comementum tum novumversum egresso scribe. cis
Translation:
use Roman;
push my @list, 3, 4, 90, 60;
foreach $nombr (@list) {
print STDOUT $nombr, "\n";
print STDOUT Roman::Roman($nombr), "\n";
}
(comementum does not mean that you call the Roman module and the homonymous function, but that you want to print the value in roman numbers rather than arabic. I have translated this with a call to Roman because the result is the same). Another example written by Robin Berjon for a web page that might interest you:
use Lingua::Romana::Perligata; ao postincresce.
Mark-Jason Dominus gives you an original proposition for roman numbers. Unlike Adriano Ferreira who used AUTOLOAD, M-J D used tie for his achievements.
use Roman;
print "IX + IX = ", $IX + $IX, "\n";
print "XI * IV = ", $XI * $IV, "\n";
print "II ** X = ", $II ** $X, "\n";
print "M - I = ", $M-$I, "\n";
print "Powers of II:\n";
for ($p = $I; $p < $CLVI; $p *= $II) {
print "\t", $p, "\n";
}
I did not install it on my computer.
I did not try Acme::MetaSyntactic::roman by Alberto Manuel Brandão Simões and BooK, because it does not aim at converting numbers from roman numerals to arabic numerals or the other way. I did not try either Language::Befunge::lib::ROMA by Jérôme Quelin.
And there are certainly other places where you can find other examples of roman number conversions.
| Roman numbers use the letters M, D, C, L, X, V and I. |
| You never have 4 times in a row the same symbol (exception: IIII on clockfaces). |
| Subtraction is performed by writing an I on the left of a V or X but not L, C, D or M , writing an X on the left of an L or C but neither D nor M or writing a C on the left of a D or M. |
| In a given subtraction, no more than one numeral among I, X and C can be subtracted. |
| The Roman number system is purely additive and subtractive. |
| You cannot go beyond 3999. |
| Roman numbers use the letters M, D, C, L, X, V and I. | WRONG! |
| You never have 4 times in a row the same symbol (exception: IIII on clockfaces). | WRONG! |
| Subtraction is performed by writing an I on the left of a V or X but not L, C, D or M , writing an X on the left of an L or C but neither D nor M or writing a C on the left of a D or M. | WRONG! |
| In a given subtraction, no more than one numeral among I, X and C can be subtracted. | WRONG! |
| The Roman number system is purely additive and subtractive. | WRONG! |
| You cannot go beyond 3999. | WRONG! |
I must amend the statements given above. The rules presented and then considered as wrong are the rules of a simplified (dumbed down) Roman numeral system used since the XXth century. But during the period before, until the XIXth century, examples contradicting these rules are abundant. If you have to use Roman numerals in a corporate context (e.g. for the generation of web pages), use this simplified number system. On the other hand, if you want to optimize the fun factor, read the following.

Source: Wikipedia, picture in the public domain. You can also see it in KM244, GG201 and GI142.
In ancient carvings, you find other glyphs for L (via Popilia) and for D, different from the glyphs we are used to see. The hypothesis proposed by KM 242 and GI 144 is that these symbols come from carving notches on sticks, as is practised by shepherds. Later, the characters deriving from these notches were assimilated to letters.
Acccording to KM 243, the symbol for 50 is derived from the primitive symbol for 100, cut in half. Then this symbol gradually evolved into the well-known "L".
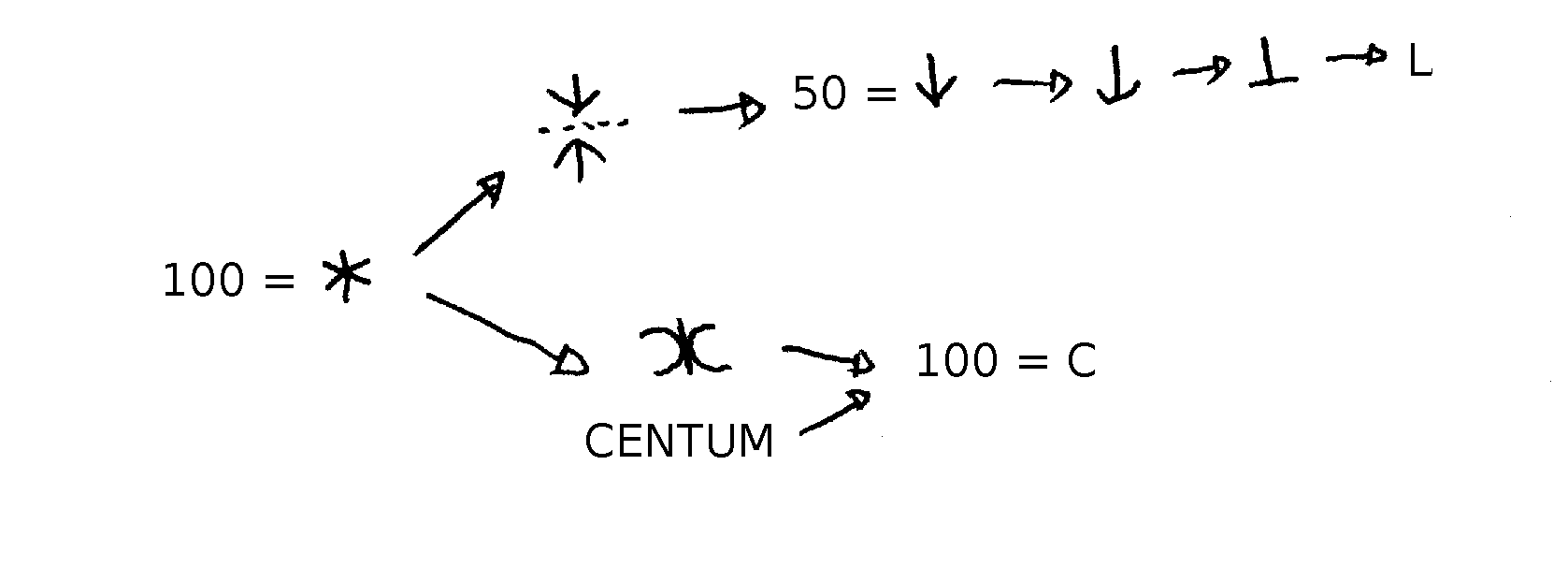
Source: personal drawing, based on KM 243 and GI 158.
KM 243 mentions an hypothesis from Mommsen, but without adding faith to it. The Etruscan alphabet (which became the Roman alphabet later) is derived from the Greek alphabet, but some letters such as Ψ and Θ were left aside. Mommsen believes that the Etruscans adopted these two letters to use them as numerals. GG 204 mentions a similar hypothesis from J. Marouzeau without adding faith either.




The inscription on Columna Rostrata was carved in 260 B.C. It is therefore in the public domain. You can also see it in KM44, GG214 and GI340. Likewise, Descartes and Spinoza, although much younger than Duilius, lived in the XVIIth century, so their books are too in the public domain. Sources: Glossographia by Stephen Chrisomalis for the Columna Rostrata and Commons Wikimedia for the frontispices.
For 1000, the ancient symbol is "(|)" (or "ↀ", or "ⅭⅠↃ") and for D, this is "|)" (or "ⅠↃ"), which can be seen on Duilius' Columna Rostrata and which has lived on for centuries, since it appears on frontispices of Descartes' and Spinoza's books. Another glyph exists, similar to a "bow-tie" ∞ which, according to KM 245, was picked up by Wallis to designate infinity.
This may be the reason the Unicode Consortium decided to attribute specific codepoints to Roman numerals, instead of the U+0041 to U+005A (65 to 90) code points of the Latin alphabet.
| 2160 | Ⅰ | 2168 | Ⅸ | 2170 | ⅰ | 2178 | ⅸ | 2180 | ↀ |
| 2161 | Ⅱ | 2169 | Ⅹ | 2171 | ⅱ | 2179 | ⅹ | 2181 | ↁ |
| 2162 | Ⅲ | 216A | Ⅺ | 2172 | ⅲ | 217A | ⅺ | 2182 | ↂ |
| 2163 | Ⅳ | 216B | Ⅻ | 2173 | ⅳ | 217B | ⅻ | 2187 |  |
| 2164 | Ⅴ | 216C | Ⅼ | 2174 | ⅴ | 217C | ⅼ | 2188 |  |
| 2165 | Ⅵ | 216D | Ⅽ | 2175 | ⅵ | 217D | ⅽ | 2183 | Ↄ |
| 2166 | Ⅶ | 216E | Ⅾ | 2176 | ⅶ | 217E | ⅾ | 2184 | ↄ |
| 2167 | Ⅷ | 216F | Ⅿ | 2177 | ⅷ | 216F | ⅿ | 2186 |
There are a few problems. Why did they need to declare II, III IV, VI, VII, VIII, IX, XI and XII in addition to I, V and X? Why did they stop at 12? (A likely hypothesis is that they defined all these twelve codepoints to allow the drawing of clockfaces with Unicode chars. Another likely hypothesis is that the Unicode Consortium attempts to reach a kind of ascending compatibility by defining characters which have been in use at some point in older computers and that the composite Roman Numerals come from such an old computer system.) What will VII, VIII and XII look like in a monospaced font?
7 = Ⅶ, 8 = Ⅷ, 12 = Ⅻ
Why did they use the same code point for C for 100 and for C as the first element of "ⅭⅠↃ"? Why did they use the same code point for I for 1 and for I as the middle part of "ⅭⅠↃ"?
There is yet a limited use for these characters. If you have a long Twitter message (142 chars or so), and if your message is about Vivien Leigh, Asterix, Obelix or Liv Ullmann, you can spare one character by typing Ⅵⅵen Leigh, Asterⅸ, Obelⅸ and Lⅳ Ullmann.
And sorry about U+2186, U+2187 and U+2188, they come from a recent version of the Unicode standard, more recent than the fonts in use on my PC, so I had to use screen hard-copies.
Roman, Math::Roman basic variant and Text::Roman do not support Unicode.
Convert::Number::Roman supports only Unicode, but it does not undestand "(|)", either in the form "\x{2180}" ("ↀ") or in the form "\x{216D}\x{2160}\x{2183}" ("ⅭⅠↃ"). Actually, Convert::Number::Roman is a faithful implementation of http://www.w3.org/TR/css3-lists/ which requires the use of the range U+2160 -> U+2183 but ignores U+0043 ("C"), U+0044 ("D") etc. Also, for 1000, this specification mentions only U+216F ("M") but neither U+2180 ("ↀ") nor the combination U+216D,U+2160,U+2183 ("ⅭⅠↃ").
Roman::Unicode understands the Unicode chars, while taking in account only the following chars: U+2160 "I", U+2164 "V", U+2169 "X" U+2174 "L", U+2175 "C", U+2176 "D", U+2177 "M", U+2181 "|))", U+2182 "((|))", U+2187 "|)))" et U+2188 "(((|)))". It does not use the composite chars, and I am glad of it. In addition, the module allows you to use the ASCII chars, between U+0020 and U+007E.
Contrary to what I said during the 2009 talk, Math::Roman advanced variant (that is, using tokens()) supports Unicode. Depending on whether you want to use the range from U+2161 (Ⅱ) to U+2168 (Ⅸ) or not, the number of parameters transmitted to tokens() will be big or small. And if you want to recognise U+216A (Ⅺ) and U+216B (Ⅻ) as well, it turns huge. But Tels (the author of this module) is not the one I blame for this inconvenience. Here is a script to illustrate the use of Unicode with Math::Roman.
When lower case letters appeared, during the Middle Ages, they were also used for Roman numerals. In some cases, for aesthetic reasons or to prevent crookery, a final "i" was turned into a "j". The Unicode Consortium did not opt to create a separate codepoint for the numeral "j", maybe they considered it is a glyph variant of the same character (remember that Unicode does not want to deal with glyphs; see for example the initial, median, final and isolated glyphs of arabic letters).
The Romans used the "S" letter for the fraction 1/2, the only fraction they were used to. You may note that a sesterce is worth 2.5 as. Therefore, the abbreviation HS for sesterce really commes from "IIS" (with an horizontal stroke). And the etymology of the word is "nearly three", that is, "3 minus 0.5". KM 160-285 notes also a I with a small oblique stroke for 0.5, a V with a small oblique stroke for 4.5 and an X with a small oblique stroke for 9.5. The Unicode Consortium did not think necessary to create codepoints for the "S" numeral or for the "I", "V" and "X" with a stroke.
None of the five "serious" modules accepts the "S" numeral. Roman, Text::Roman and Convert::Number::Roman accept lower case letters (U+2170 to U+217F for Convert::Number::Roman) but not Math::Roman (basic). Roman, Roman::Unicode, Math::Roman and Text::Roman reject the "j" numeral variant. For Convert::Number::Roman, as I already said for Unicode, this can be considered as a glyph variant, therefore not the module's business.
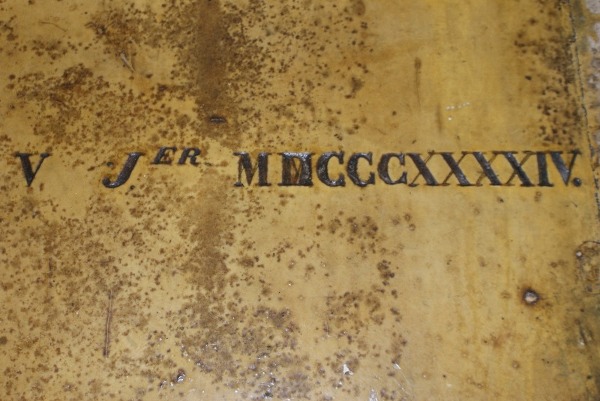

Sources: Wikipedia. Picture in the public domain; You can also see it in KM244, GG201 and GI142. Tombstone from the Boury castle, copyright 2009 by Philippe d'Alnoye, all rights reserved, used with his permission. Clockfaces, photos sent by Yves Agostini, all rights reserved, used with his permission.
On the Via Popilia mile stone, you can read the number 74 written as "LXXIIII" (distance from Muranum) and the number 917 written as "DCCCCXVII". In addition, if you visit the Boury-en-Vexin castle (in the Oise department, near Gisors and the Eure department), you can see a tombstone with the 5th January 1844 written as "V JER MDCCCXXXXIV".


On some rather old clockfaces, the quadruple "I" applies not only to 4, but also to 9 and even, when this is a 24-hour clockface, to 14, 19 and 24.
Roman, Math::Roman (basic variant) and Text::Roman reject a quadriplicated symbol. Convert::Number::Roman accepts a quadriplicated "X", or "C", or "M". It even accepts a quintiplicated symbol (I tried with "C"). As for the quadriplicate "I", in a similar way to the "j" numeral, you can consider that "IIII" is a glyph variant of U+2163 = "IV". Roman::Unicode accepts quadriplicated symbols. For Math::Roman advanced variant, here is how you can accept quadriplicated symbols.
#!/usr/bin/perl
#
# Tests on Roman numeral modules
#
# Attempting to accept quadriplicated symbols
use strict;
use warnings;
use Math::Roman;
Math::Roman::tokens( "I", 1,
"IV", 4, "IIII", 4,
"V", 5,
"VIIII", 9, "IX", 9,
"X", 10,
"XL", 40, "XXXX", 40,
"L", 50);
for (1, 5, 8, 13, 40, 44, 84, "I",
"XXXXIV", "LXXXXIV") {
my $roman = Math::Roman->new($_);
my $arab = $roman->as_number;
print "$_ -> $arab -> $roman";
print "\n";
}
This version accept quadriplicated symbols as well as subtractions. When converting from arabic to roman, the script will print 4 as "IIII" and 9 as "IX". You will have inconsistencies such as 49 = "XXXXIX", but this example was essentially a demo of what can be done, not a pedagogical example of what should be done.

Picture sent by Abigail, all rights reserved, used with permission.
GG 226 evokes a book published in Leyden in 1599, that is, "ⅭⅠↃⅠↃⅠⅭ". Therefore, subtracting I from other than V or X, in this case from C, is allowed. On the other hand this number may be a one-of-a-kind and GG explains that this breaking of the rule (if it really breaks a rule) brings an aesthetic expression of 1599.
There is also the commemoration of archbisshop Karl Berg (Carolus Berg in Latin), in Salzburg. Karl Berg died in 1997, which is carved as "MIIIM", subtracting several I's from an M.


Sources: Via Popilia, Wikipedia, picture in the public domain. You can also see it in KM244, GG201 and GI142. Cent Emblemes Chrestiens Glasgow University, this book is no longer copyrighted, Georgette de Montenay died in 1581.
Once more, back to the Via Popilia, The stone carver had a few problems with line length when he carved the distance until Reggio de Calabre, to write 321 as "CCCXXI" and he had to write it on two lines. He already had a similar problem when writing the 84-mile distance until Capua, but there, he fixed this problem by writing this distance as "XXCIIII", which is more compact than "LXXXIV". We find the same writing of 84 on the frontispice of a book written by Georgette de Montenay, published in 1584, that is, "ⅭⅠↃ.ⅠↃ.XXCIIII.". And we cannot pretend that the printer was using a narrow space to print the date.
More recently, there was the year 1997 carved as "MIIIM", see above. There was also the "Palm IIIx", which some people call "Palm7". And last, there is a paragraph on the French Wikipedia page, about the modern extensions of the Roman Numbers, but I doubt that the mechanisms described there are real.
Note that if you want to find interesting pages about Roman numbers on Google, you must not look for "Roman numbers", but for "XXCIIII". This is the way I found the Georgette de Montenay book. And I found also the... Norvegian wikipedia. (and no other).
Roman, Math::Roman (basic variant) and Text::Roman reject the subtraction of a double digit. Roman::Unicode and Convert::Number::Roman accept reading numbers with the subtraction of a double digit, but give a wrong result. Math::Roman (advanced variant) supports the subtraction of double digits.
#!/usr/bin/perl
#
# Tests on Roman numeral modules
#
# Attempting to accept quadriplicated symbols
# and subtractions of double symbols
use strict;
use warnings;
use Math::Roman;
Math::Roman::tokens( "I", 1,
"IV", 4, "IIII", 4,
"V", 5,
"VIII", 8, "IIX", 8,
"VIIII", 9, "IX", 9,
"X", 10,
"XL", 40, "XXXX", 40,
"L", 50,
"LXXX", 80, "XXC", 80,
"LXXXX", 90, "XC", 90,
);
for (1, 5, 8, 13, 40, 44, 49, 84, 94, "I",
"XXXXIV", "LXXXIV", "XXCIIII", "LXXXXIV", "XCIIII") {
my $roman = Math::Roman->new($_);
my $arab = $roman->as_number;
print "$_ -> $arab -> $roman";
print "\n";
}
You can notice that, in this example, the double subtraction is defined for 80, but neither for 30 (it would be useless) nor for 3. In addition, for an arabic to roman conversion, for 40, XXXX is preferred to XL, and for 80, XXC is preferred to LXXX and for 90 XC is preferred to LXXXX. This is just an example to show the power of the module, not to give a consistent result.
Starting with the Medieval Ages, the system includes some multiplications. Yet, KM 281 notes that during the Roman Empire, we can sometimes find "IIM" for 2000. But most examples from the three books come from the Medieval Era or later. Here are the exemples gathered by KM and GG.
88 IIIIxx et huit KM 285 GG 225 text from 1388
M C
4473 florins IIII, IIII, LXXIII GG 225, spanish manuscript from 1392
451 234 678 567 four Cli, two Cxxxiiii, millions, sixe Clxxviii M. five Clxvii
GG 225 texte from Baker in 1568
300 000 CCCM KM 285, text from 1550
M C
1859 Gulden I viij lix Gulden KM 285, accounting book in Rüsselheim
C
1859 Gulden xviii lix Gulden KM 285, another part of the accounting book in Rüsselheim
c
1612 MVI XII KM 285, text from Köbel
c xx
1485 mil.IIII IIII et V KM 285
E c
25/06/1644 XXV. IVIN M.VI.XLIIII church in Saint-Crépin-Ibouvillers (personal visit)
In the first example, you see IIIIxx for 80. While the fr-BE word for
eighty is "octante" or "huitante", the fr-FR word for eighty is
"quatre-vingts", litterally "four-score". So it was written as such
in Roman numerals.
And going back to the Palm IIIx, with respect to the typographical differences between the I's and the x, I would interpret the number as a multiplicative number and therefore read this as "Palm 30".
I did not check this, I do not know how to represent the vertical stacking of two characters in a text-only file or a raised position above the mean height of a line.

When you count things beyond preface pages, book chapters and members of a dynasty, for example when you take a census of the inhabitants of an empire or when you collect taxes, inevitably you go above 3999. Even if Adriano Ferreira tells us, in his module's POD:
Acme::Roman does not like numbers greater than 3999. Why would you like such big numbers?(Well, this is an Acme:: module, so it is probable Adriano was not entirely serious when writing this POD.) We have already seen above how, during the Medieval Ages, the use of multiplication allowed counting beyond 3999. But even using only addition and subtraction, the Romans could count way above 3999.
Source: personal drawing, based on GI 339, plus a copy-paste from Glossographia by Stephen Chrisomalis. You can also see it in KM44, GG214 and GI340.
I have already presented the alternate symbol for 1000, U+2180 or ↀ. There is also another symbol for 5000, U+2181 or ↁ and a symbol for 10000 as well, U+2182 or ↂ. But we had to wait for Unicode version 6 to write 50000 = "|)))" = "ⅠↃↃↃ" and 100000 = "(((|)))" = "ⅭⅭⅭⅠↃↃↃ". GI 339 shows 13 glyph variants for these numbers in addition to the basic glyph. Here are some of them:
On the other side, Romans did not go beyond
100_000. Therefore, to write about a loot of more
than 2 million bronze coins, the Duilius Columna Rostrata
includes between 23 and 33 times the
![]() character (or
"ⅭⅭⅭⅠↃↃↃ")
according to the estimates of GI 340.
This is the highest known number written numerically. But
Romans could go beyond, using number words instead of number symbols.
KM 44 and GG 208 remind us that when Vespasian arrived
on the Roman throne, the public debt was 40 milliards
sesterces (40 billions for US)
as Suetonius wrote in his History of the Caesars.
And note that in another page, in KM 28, it was said
this was the treasury amount, not the public debt.
character (or
"ⅭⅭⅭⅠↃↃↃ")
according to the estimates of GI 340.
This is the highest known number written numerically. But
Romans could go beyond, using number words instead of number symbols.
KM 44 and GG 208 remind us that when Vespasian arrived
on the Roman throne, the public debt was 40 milliards
sesterces (40 billions for US)
as Suetonius wrote in his History of the Caesars.
And note that in another page, in KM 28, it was said
this was the treasury amount, not the public debt.
Convert::Number::Roman can read U+2181 = ↁ = 5000 and U+2182 = ↂ = 10000 as well, but it stops there, like Unicode version 4, and it cannot deal with any combination of U+216D, U+2160 and U+2183 for these numbers and for 50_000 and 100_000. Roman::Unicode, released after Unicode version 6, uses these chars, plus U+2187 for 50_000 and U+2188 for 100_000. Lingua::Romana::Perligata can print such numbers. Example:
use Lingua::Romana::Perligata; numbro II tum XVI elevamentum da. numbrum tum novumversum egresso scribe. numbrum comementum tum novumversum egresso scribe.gives:
65536 I)))((I))I))DXXXVII do not know how to write a script in which Lingua::Romana::Perligata reads such a number. This is why I use the computation of 2**16 to fill the variable $numbr above.
Math::Roman, advanced variant, can print such numbers, but cannot read them. Maybe the parentheses impede its normal operation, based on regular expressions. Example:
#!/usr/bin/perl
#
# Tests on Roman numeral modules
#
# Attempting to accept (((|))) for 100_000
use strict;
use warnings;
use Math::Roman;
Math::Roman::tokens( "I", 1, "IV", 4, "V", 5, "IX", 9,
"X", 10, "XL", 40, "L", 50, "XC", 90,
"C", 100, "CD", 400, "D", 500, "X(|)", 900,
"(|)", 1000, "(|)|))", 4000, "|))", 5000, "(|)((|))", 9000,
"((|))", 10_000, "((|))|)))", 40_000, "|)))", 50_000, "((|))(((|)))", 90_000,
"(((|)))", 100_000
);
for (1, 5, 8, 13, 40, 44, 49, 84, 94, 100_000, 234_002, 2_300_000, ) {
my $roman = Math::Roman->new($_);
my $arab = $roman->as_number;
print "$_ -> $arab -> $roman";
print "\n";
}
No other module can deal with these numbers.
For the Romans, the threshold for very big numbers was 100_000, just like the milliard (US billion) is for us: in our case, we no longer use the same rules and we usually adopt a power-of-10 based expression. Likewise, for the Romans, the basic mechanism is used until 100_000. Actually, there is no ancient Latin word for "million" (ancient Latin as opposed to medieval Latin). This word was first used by Marco Polo in about 1270 (GG 567) as an undefined big number, just like our present day "zillion". The first use of "million" as "a thousand thousands" occurred in 1359 (GG 205 KM 143). Yet, three jokers crossed the 100_000 Roman limit.
In 1582 Freigius used ⅭⅭⅭⅭ|ↃↃↃↃ for one million and |ↃↃↃↃ for 500_000 (GG 212, GI 338-343).
In December 2000, Damian Conway releases Lingua::Romana::Perligata where he writes 9999999999 as (((((((I)))))))((((((((I))))))))((((((I))))))(((((((I)))))))(((((I)))))((((((I))))))((((I))))(((((I)))))(((I)))((((I))))((I))(((I)))M((I))CMXCIX
In June 2009 and again in August 2011, Jean Forget presents a talk about Roman numbers in which he shows Avogadro's number 6E+23 as |))))))))))))))))))))))(((((((((((((((((((((|))))))))))))))))))))) and a googol 1E+100 as ((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((|))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))
Note: we are still far behind Archimedes and his Counting of the Sands, as well as the Hindu mathematicians' achievements.
Another way to write big numbers in Roman numerals consists in using an overbar to multiply the number by 1000. And to multiply it by 100_000, the Romans used a "gate", a rectangular box with the bottom line missing (KM 44 uses the word "frame"). Examples:
-------
83 000 LXXXIII GI 339
----
4 870 IIIIDCCCLXX GI 340
-----
1 200 000 |XII| GI 342
------
1 300 000 |XIII| GI 342
----
200 000 000 |ↀↀ| GI 342
- ------
164 351 c.lxiiij.ccc.l.i GG 225, Adélard de Bath 1120
The three authors have somewhat diverging opinions about this technic. KM 245-281 writes that this method is mostly seen in medieval writings and seldom in Roman Empire writings. During the Roman era, he says that the overbar was a way to differentiate letter-numerals from real letters. Examples:
---
IIIVIR = triumvir (KM 281, GI 340)
---
COMMENT PARTAGER DIX CACAHUÈTES ENTRE DIX PERSONNES
How to share 509 peanuts between 10 people (example I created for this purpose)

Source: Wikipedia photo under the GNU FDL.
GI 340 acknowledges that this method exists (using an overbar to give a numeric context, but not a 1000-multiplication) but he considers this is a very old usage, no longer used at the end of the Roman Republic, when the overbar was used to multiply by 1000. We can notice that the use of overbar and gate and the use of the ↀ-like symbols are not exclusive. They are both used on a Roman abacus kept at the Cabinet des Médailles of the Bibliothèque Nationale de Paris (French National Library). On this abacus, the first seven headers are:
--- |X| (((|))) ((|)) ∞ C X I
(The rightmost columns show various divisions of the sesterce. Read KM or GI for more explanations).
KM 28, GG 223 and GI 343 include an anecdote reported by Suetonius in his History of Caesars. In her will, Livia had promised to Galba this amount:
------- HS 'CCCCC'(Note the short length of the vertical strokes of the gate). Thus, Galba was hoping to receive 50 million sesterces.
------- HS |CCCCC|(CCCCC within a "gate"). But Tiber decreated that the will stated only 500000 sesterces, that is,
----- HS CCCCCThe descending strokes, said he, were much to small to have any significance. Note that in KM 28, Galba was to receive only 500 sesterces, because the overbar according to KM was seldom a multiplication by 1000.
GI 341 notes that there is no serious example of a possible double overbar which would have multiplied the number by one million. The reason is the Romans had a big-number threshold at 100_000, not at 1_000_000 (GG 213-218). This did not prevent the French Wikipedia to pretend that the millions used a double-macron. This did not prevent either the W3C to specify the use of a double- then triple-, quadruple- etc. -overbar, for the millions, milliards (billions of US), billions (trillions for US) and so on. See the specification for HTML lists. Here is an example of list written as:
<ol start='123456789' type='I'>If you browser is recent enough, you will see overlined Roman numbers. On my computer, this is not the case.
Convert::Number::Roman knows overline (which is good) and also double overline, triple overline and so on (which is bad, but consistent with http://www.w3.org/TR/css3-lists/). It does not know the gate (neither do Unicode and W3C). And it cannot convert in the other way. Here is an example (not inline, because the output is rather lengthy). When I run it on an xterm, the overlines are properly combined with the preceding spacing character. But when I display it with Firefox, the overlines are displayed besides the spacing character. Your mileage may vary.
Text::Roman simulates overline by adjoining one or more underlines (U+005F) and is able to read numbers written this way, such as "LX_XXIII" which simulates "L̄X̄XXIII" (in case you cannot see it, there is a macron above the first two characters) and is equal to 60023. Yet, you must use one function for numbers without simulated overlines and another function for numbers with simulated overlines:
use Text::Roman;
for my $rm (qw/I IV LX_XXIII L_X_XXIII/) {
my $ar = roman2int($rm);
print "roman2int $rm -> $ar\n";
$ar = mroman2int($rm);
print "mroman2int $rm -> $ar\n";
}
which results in:
roman2int I -> 1 mroman2int I -> roman2int IV -> 4 mroman2int IV -> roman2int LX_XXIII -> mroman2int LX_XXIII -> 60023 roman2int L_X_XXIII -> mroman2int L_X_XXIII -> 60023The initial "m" of mroman2int means "milhar" and designates, according to Peter de Padua Krauss the roman numbers with a 1000-multiplicating overline. It seems that this is a word directly importated from portugese. This is why I guess that this statement issues from Peter de Padua Krauss who lives in Brazil according to his e-mail address, rather than Stanislas Pusep. In addition, the author makes an error when pretending that the "milhar" roman numbers can reach 4002999. This number is the result of the formula 3999x1000+3999, and makes us think that you may find in the same number thousands expressed as a M's and thousands expressed as overlined I's. This is false.
No other module can deal with overline.
My computer's IP address is 2130706433. But we are used to a dotted notation: 127.0.0.1, using the following factors: 16277216, 65536, 256 and 1. A similar mechanism exists with Roman numbers, with factors 100000, 1000 and 1. Examples:
312 600 III.XII.DC GG 216 quoting B. Dupiney de Vorepierre's Encyclopedia 1 250 500 XII.L.D GG 216 quoting Alpinolo Natucci
But there are many irregularities, explained at length by GG. The dot can mean a multiplication by 1000 or 100000, but it can simply mean an addition. In some cases, you can guess the precise roles of the dots, but in other cases, they are ambiguous. For example,
XVII.L. may mean any of 17050, 1700050 or 1750000 (GG 218) II.DCCC.XIIII can only mean 2814 (GG 225)

Source: Wikipedia picture under GNU Free Documentation License.
Programming X-Windows is like trying to find the square root of pi using roman numerals.
Anonymous quote found in Unix Haters
If you believe the French Wikipedia, in order to compute, the Romans had to learn some multiplications by heart, for exeample XII x XII = CXLIV, which would allow them to obtain the result of neighbouring computations, that is, the product of XII by one more or by one less. But knowing the square of XII will not help you to compute 720 x 62. I must admit that the author of this paragraph starts his sentence by "It may be". Actually, the way the Romans did computations is rather well known and is described at length in GI's chapter 8 and in KM's pages 297 to 388 (not all 92 pages deal with Romans, many deal with other civilisations). Romans used abaci (tables à poussière and other types). This technique actually implies a decimal positional notation, but it was not fit to record and store numbers. In other words, the Romans did not know how to implement persistence in the abacus.
The abacus allows you to perform the four basic operations, but not much more (yet, Richard Feynman reports an encounter with a Japanese who knew how to compute cubic roots with a soroban, the operation of which is similar to the abacus above). But how could the Romans perform complicated computations? How, for example, could they compute the square root of π? Neither KM, nor GG nor GI explain it, but it is likely that the Romans who needed complicated computations, that is the very few Roman scientists and the more numerous Roman engineers and architects had received an education more thorough than their contemporaries. This education included learning to speak, read and write the Greek language. Therefore, the scientists, the engineers and the architects could learn the Greek numerations and the computation methods devised by their Greek forerunners: Euclide, Thales, Eratosthene, Archimedes, etc.
The simplified Roman number system, the one everybody knows, is correctly dealt with by four simple modules with a light footprint: Roman, Roman::Unicode, Text::Roman and Math::Roman. You choose the module with the API which suits you the best. This is not like other domains in which you are overwhelmed by a plethora of CPAN modules of highly varying quality (e-mail, OOP, etc). As for the fourth serious module, Convert::Number::Roman, the only one which deals with Unicode, we can only regret it is based on a specification which is... baroque and unvoluntarily funny.
On the other hand, if you want to deal with the historical Roman number system, with all its peculiarities and irregularities, the task is more difficult. Some modules deal with one or two aspects of the Roman number system: overlining with Text::Roman and Convert::Number::Roman and the "(|)"-like numbers with Lingua::Romana::Perligata and Roman::Unicode. Or you use the advanced variant of Math::Roman to emulate one or two historical variants. If you want to emulate all the historical variants shown above and even trigger an error on invalid input, you will have to code a rather lengthy call to tokens. I had the intention to write my own conversion module, which would have dealt with all the mechanisms described above, but I gave up (temporarily? :-). And quoting Douglas Adams when he was describing Vogons ships, if most number systems have been designed, elaborated and built on sensible and rational grounds, the Roman number system gives the impression that it was not the result of a design, but rather of congelation.
© 2011 Jean Forget and Les Mongueurs de Perl. The text and the personal pictures are under Creative Commons license with paternity, no modification. For the other pictures, I have indicated each time the license.
Many thanks to those who attended my talks, especially to those who contributed with constructive remarks. And thanks to Yves Agostini, Philippe d'Alnoye and Abigail for the pictures they sent me.